Els nens comencen a estudiar les formes i els colors des de la infància utilitzant diverses tècniques, en particular, a través d'apliques. Aquestes aplicacions estan fetes de formes geomètriques que el nen enganxa a una base de cartró o paper.
A quina edat pots començar a ensenyar formes geomètriques al teu fill/a?
Segons els científics, un nen ha de rebre educació des del naixement, i això es duu a terme en diverses etapes:
- Després del naixement, el nadó no recorda gairebé res, però aprèn a mirar el món en tots els seus aspectes. En aquest moment, es recomana parlar amb el nadó, pronunciar cada figura, llegir poemes infantils curts i cantar cançons.
- Quan el nadó compleixi 6 mesos, intentarà aprendre més sobre el món. Per fer això, tocarà i mossegarà objectes. És important triar les joguines adequades. Un conjunt de quadrats suaus amb flors, papallones i ocells dibuixats hi haurà bé.
- La següent etapa comença quan el nadó aprèn a parlar. Cal pronunciar tots els noms de les figures, començant per les més simples (cercle, triangle, quadrat). Després arriba el torn del trapezoide, rectangle i altres. En aquesta etapa, una piràmide de joguina, blocs de plàstic utilitzats per construir una torre i dibuix ajudaran.

Així, l'entrenament es pot fer des del naixement d'un infant, utilitzant diferents mètodes.
Aprenentatge de formes geomètriques: noms, formes, colors, mides
A mesura que el nen creix, hauria de reconèixer més i més formes i colors.
Als 2 anys has de saber:
- triangle;
- quadrat;
- cercle.
A aquesta edat, cal conèixer els colors bàsics:
- blau;
- vermell;
- groc;
- verd;
- blanc.
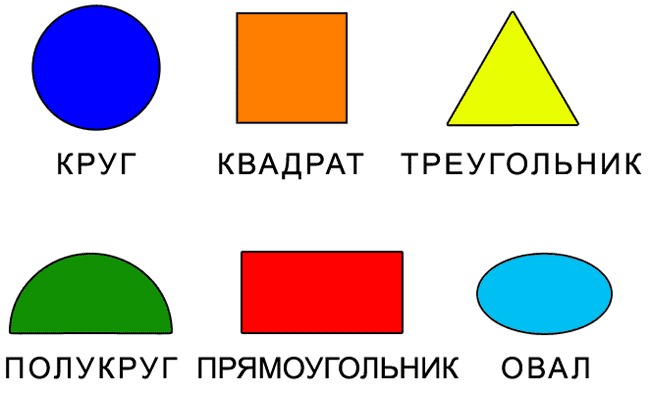
Alguns nens de 2 anys coneixen alguns colors més:
- taronja;
- violeta;
- negre;
- rosa.
Als 6 anys, el nen aprèn sobre colors i tons combinats més complexos, i es familiaritza amb figures compostes (que consisteixen en figures bàsiques).
Els nens aprenen a través de jocs, que tenen diferents nivells de dificultat, per la qual cosa es recomana donar-los-hi en la següent seqüència:
- Cercles, triangles, quadrats de diferents mides i colors dibuixats sobre cartolina. Digueu les imatges pel seu nom, dient-les en veu alta.
- Dibuixa només els contorns de les figures en cartró, i tots els contorns han de ser de diferents colors, de manera que el nen pugui resseguir-los amb els colors corresponents, pintar-los i dir-ne els noms en veu alta. A partir dels 2 anys, hauries de començar a comparar les talles.

- Retalla les figures i col·loca-les en llocs visibles de la casa perquè el nen pugui buscar les imatges. Cada vegada que el nen trobi una imatge, ha d'anomenar les següents característiques: forma, color i mida.
- Conjunts de joc dissenyats per explorar l'anterior. Per exemple, una piràmide, bolets de diferents colors i mides en un suport, un mosaic i altres. Aquests jocs entretindran el nen i atrauran la seva atenció.
- Busca formes geomètriques en el món que l'envolta. Per exemple, una taula és un rectangle, una caixa és un quadrat i una pilota és un cercle. Es recomana tenir en compte formes més complexes: un got és un cilindre i una tapa de festa és una piràmide.
S'han desenvolupat moltes tècniques per estudiar formes i colors. Estan dissenyats per a nens de diferents edats i també tenen en compte les seves activitats preferides.
Aprenentatge de formes geomètriques complexes amb formes simples: beneficis de les classes per a nens
Les formes geomètriques, o formes compostes, són més fàcils d'aprendre a través de formes simples. Cal retallar diversos quadrats, cercles i triangles i plegar-los.
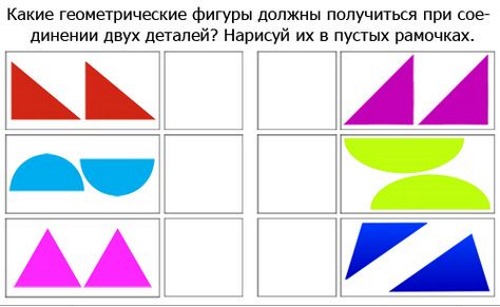
Exemples de creació de figures complexes:
- Trapezoide: quadrat + 2 triangles.
- Rectangle: 2 o més quadrats.
- Rombe: 2 triangles iguals.
- Paral·lelogram: 2 quadrats + 2 triangles iguals.
L'infant ha d'estar completament involucrat en el procés d'aprenentatge, altrament l'aprenentatge serà inútil. Aprendre a través del joc és la millor manera d'atreure l'atenció de l'alumne i fer que el procés sigui interessant. En fer descobriments pel seu compte, el nen voldrà continuar aprenent.
Lliçons de geometria descriptiva per a nens
La geometria descriptiva té com a objectiu desenvolupar el pensament espacial. El nen aprèn a imaginar figures tridimensionals complexes descomponent-les en figures simples i planes. Les tasques no només requereixen triar les respostes correctes, sinó també explicar la teva elecció i per què les altres respostes són incorrectes.
Completa la figura utilitzant l'exemple
Dibuixar ajudarà a reforçar la lliçó.
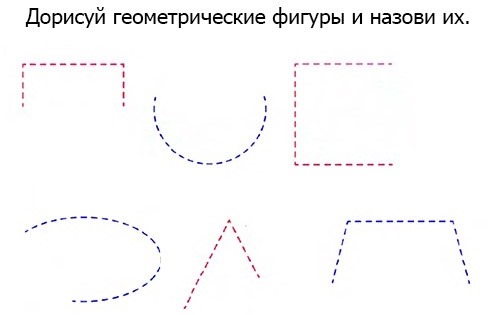
Què cal fer:
- Mostra al nen les formes, explica-li-les, dóna exemples de coses de la forma corresponent que hi hagi a l'habitació.
- Imprimiu formularis en què es representen les figures inacabades amb una línia de punts (a dalt es mostra un exemple de formulari).
- Tasca: continua la línia de punts, digues quina imatge és un cercle, un quadrat o un rectangle.
- Discutiu els resultats obtinguts.

En lloc de línies de punts, hi pot haver línies regulars, però interrompudes. Aquesta és una versió simplificada de l'exercici. Per fer la tasca més difícil, heu d'imprimir un formulari en què la part de la figura estigui acolorida, però no repeteixi els contorns. Això confondrà el nadó.
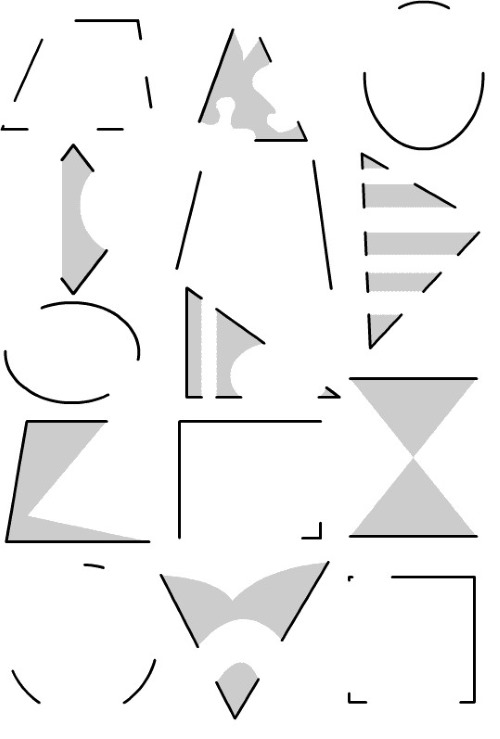
A més d'acabar el dibuix, cal pintar la part restant de la figura.
Traçar una figura per punts
L'exercici d'unir els punts desenvolupa la teva imaginació permetent-te imaginar quins punts cal connectar per crear una figura determinada. Aquesta habilitat desenvolupa la capacitat de completar tasques segons un model, cosa que serà útil a l'escola. El nen ha de dibuixar amb un llapis per poder corregir els errors.
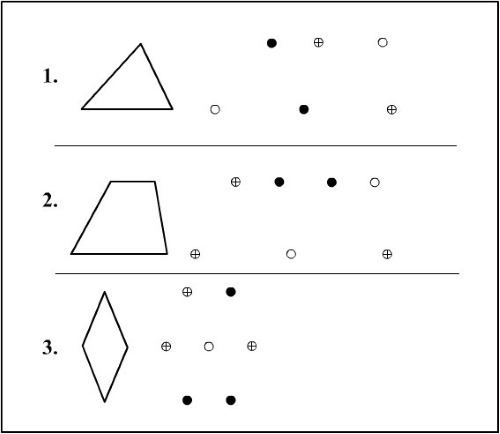
Com fer l'exercici:
- Imprimeix els formularis de les tasques.
- A cada formulari, a l'esquerra, hi ha un dibuix de mostra, i a la dreta, hi ha diversos punts a partir dels quals cal crear el mateix dibuix.
- El nen ha de notar que els punts són diferents: hi ha punts amb creus, punts negres i punts blancs. No es poden connectar punts idèntics.
- A la dreta hi ha més punts dels necessaris; alguns romandran fora del dibuix.
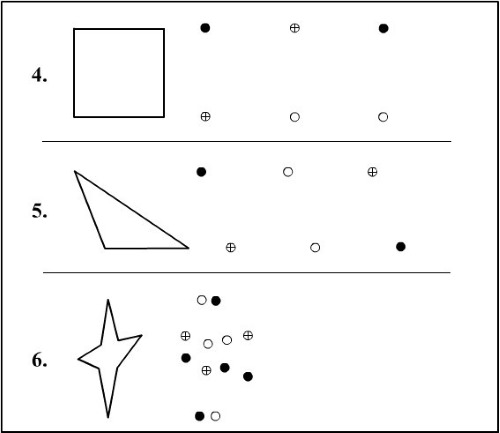
Trobar formes geomètriques en una imatge
Les formes geomètriques atrauen l'atenció dels nens. S'interessen per com dividir un dibuix complex en un de simple i com muntar un de simple en un de complex. Aquesta tasca et demana que trobis cercles, quadrats i triangles. En una versió més complexa, s'afegeixen rectangles, trapezoides, ovals i rombes.
Dibuix fàcil de papallones per a noies:
- Cercles de diferents mides: el cos.
- 2 parells de triangles idèntics: ales inferiors i superiors.
- 2 peces de cercles petits, mitjans i grans: decoració de les ales.

En el dibuix "casa" podeu trobar:
- La plaça és la part principal de la casa.
- El rectangle és la porta.
- Dos cercles o ovals són finestres.
- El cercle petit és el mànec de la porta.
- El triangle és el sostre.
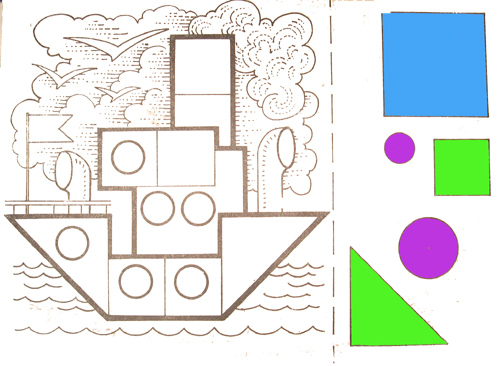
Patró avançat de "vaixell":
- El trapezoide és el buc d'un vaixell.
- 3 cercles – finestres de cabina.
- 2 rectangles de diferents mides - elevació a la coberta.
- Els triangles són veles.
Dibuix "robot":
- El quadrat és el cos del robot.
- 2 rectangles iguals – potes.
- 2 triangles equilàters idèntics – peus.
- 2 diamants iguals: botons al cos del robot.
- Rectangle llarg – espatlles.
- 2 cercles, 2 rectangles i 2 cercles – braços.
- Un petit quadrat és la cara.
- 2 cercles petits – ulls.
- El triangle és el nas.
- El rectangle prim és la boca.
- Trapezoide (la longitud ha de ser més llarga que el quadrat de la cara) – barret.
Els exemples de dibuixos estan ordenats segons el nivell de dificultat (de fàcil a difícil).
Pintar formes geomètriques
La tasca desenvolupa el pensament espacial, ja que el nen ha de pintar les figures de manera que una se superposi a l'altra.
Com realitzar l'exercici:
- Dibuixa parelles de cercle-quadrat, triangle-cercle, quadrat-triangle i altres en un full de paper de manera que els seus extrems s'intersequin i se superposin.
- Doneu al nen/a un full de paper i llapis de colors.
- Demana al teu fill/a que pinti les figures de manera que una de la parella estigui a sobre de l'altra, dient els colors en veu alta.
Per facilitar la tasca, cal mostrar al nen les figures tridimensionals amb antelació, donar-li l'oportunitat de moure-les i jugar-hi.
Trencaclosques de formes geomètriques: com unir les formes correctes
Les formes geomètriques no són immediatament clares per als nens. Per simplificar l'aprenentatge, es recomana muntar una mena de "trencaclosques".

Com realitzar la primera versió de l'exercici:
- Imprimeix formularis amb formes simples dibuixades a la part superior i diverses formes complexes a la part inferior.
- El nen ha de trobar quina de les opcions de la part inferior del full combina totes les formes enumerades a la part superior del full.
- També cal explicar les respostes obtingudes.
Al principi, hauríeu de fer dibuixos senzills en què les figures estiguin connectades sense inclinar-se. A més, la forma només pot contenir quadrats o només triangles.
L'exercici desenvolupa la imaginació i l'orientació en el pla de les figures.
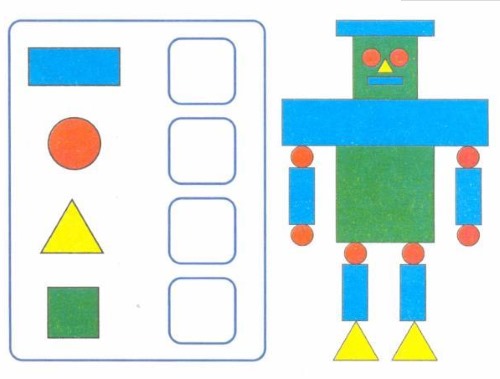
Agrupar formes simples en formes complexes
Aquesta tasca és la inversa de l'anterior.
Com realitzar l'exercici:
- Imprimeix diversos cercles, quadrats, triangles i trapezoides en cartró i retalla'ls.
- La tasca del nen és crear tantes formes diferents com sigui possible, que consisteixin en les figures enumerades anteriorment.
- Per aprendre els nombres, cal comptar cada tipus de xifra.
Per fer la tasca més difícil, el nen ha de fer un dibuix específic (un ocell, un vaixell).
Segona opció per realitzar l'exercici:
- Mostra al nen la imatge en color i proporciona les formes necessàries per completar el dibuix.
- La tasca és crear una imatge idèntica.
Aquesta opció està pensada per a nens de 6 anys o més.
Exemples i instruccions pas a pas per crear aplicacions a partir de formes geomètriques
Segons l'edat del nen, les aplicacions es realitzen de manera diferent:
- Els nens menors de 2,5 anys no saben tallar, així que ho fa un adult. A criteri de l'adult, el nen o l'adult pot enganxar les parts de paper al cartró. En el segon cas, hauríeu de consultar amb el vostre fill sobre on enganxar exactament la peça.
- Els nens de 2,5 a 5 anys poden tallar amb tisores, però ho fan de manera desigual, per la qual cosa si cal, cal corregir la irregularitat.
- A partir dels 5 anys, els nens aprenen a tallar de manera uniforme, per la qual cosa la participació dels adults en el procés de creació d'una aplicació és mínima.

A una edat primerenca, un nen intenta simplificar la forma que veu. Per exemple, els núvols que semblen rínxols es simplifiquen en un oval.
Per a nens de 3 a 5 anys
Les imatges inusuals i el procés de la seva creació poden atraure els nens petits. L'aplicació "Eriçó" no és estàndard, però és fàcil de crear. Com a agulles s'utilitzen palmes de paper marró o negre.
Es poden fer de dues maneres:
- Col·loca el palmell de la mà del nen al revers del paper i traça'n el contorn amb un llapis simple. Retalla el palmell de la mà seguint el contorn.
- Pinta el palmell de la mà del nadó amb pintura i col·loca-ho sobre el paper. No cal delinear els contorns. Retalla la peça.
Necessitareu 4 palmells.
També necessitareu les peces següents:
- "Vaixell" format per un oval i un triangle corbat. Aquesta peça servirà com a cos i nas de l'eriçó.

- Un petit cercle és la punta del nas.
- El semicercle vermell és la boca.
- El semicercle blanc forma part de l'ull.
- El petit cercle negre és la pupil·la.
- Un cercle amb una part superior i inferior tallades en verd és una poma.
- Diamants de color verd fosc: 2 fulles de poma.
- El detall que sembla una càpsula blanca és la tija del bolet.
- El semicercle marró és la gorra de bolet.
- Quatre trapezoides de diferents mides són les potes.
Les peces s'han d'enganxar en l'ordre en què s'enumeren a dalt. En aquest cas, es col·loquen 2 palmells amb els dits apuntant cap amunt, un en diagonal i l'últim cap al costat.
L'extrem del cos es troba a prop de l'últim palmell.
Aplicació "Marieta volumètrica":
- La meitat de l'oval negre és el cap.

- Dos cercles vermells o roses: cos. Els cercles s'han de plegar per la meitat: enganxeu una meitat al cartró i deixeu l'altra. Enganxa la meitat del segon cercle al costat del primer de manera que la part enganxada formi un cercle.
- Els cercles negres són punts. Es troben tant a les parts enganxades com a les que retrocedeixen del cos.
- Ulls comprats de diferents mides.
- Dibuixa les antenes i els cercles als seus extrems amb un retolador negre.
La pintura atrau pel seu volum. El nen pot jugar amb les parts que sobresurten de la marieta.
Com fer l'aplicació "prat de flors":
- Pinta el full de cartró de verd.
- Doblegueu un quadrat petit 4 vegades per fer un quadrat més petit. Retalla 3 cantonades (excepte la cantonada plegada). Desplega el full.
- Enganxa un cercle d'un color contrastant al centre dels pètals obtinguts del quadrat.
- Fes algunes flors.
- Enganxa les flors sobre un tros de cartró pintat.

La imatge serà multicolor, de manera que el nen estarà interessat a mirar les flors de més a prop.
Per a alumnes de 1r de primària
Els alumnes de primer de primària poden crear aplicacions més complexes utilitzant materials nous.
Aplicació "Lila":
- Pinta un tros de cartró amb pintura d'aquarel·la. Si ho desitgeu, podeu fer una transició suau d'un color a un altre (de vermell a morat, de morat a blau o de blau a blau pàl·lid).
- Deixa que el fons s'assequi.
- Retalla un rectangle i un cercle per al gerro.
- Enganxa primer el rectangle a la base i el cercle a sobre.
- Talla 4 tires primes i curtes de paper ondulat verd. Aquestes tires seran les tiges.
- Enganxa les tiges uniformement a l'extrem del gerro.
- Retalla 6 peces ovalades o en forma d'ou d'un tovalló de color. Aquests detalls ajudaran a marcar els límits de les inflorescències liles.

- Enganxa les peces al costat de les tiges. Com que hi ha més inflorescències que tiges, cal fer coincidir 4 inflorescències amb tiges i enganxar la resta a les vores del gerro.
- Talleu els tovallons en quadrats petits.
- Alguns d'ells estan arrugats en quadrats, la resta primer estan esquinçats i després s'arrugaven.
- Unteu la inflorescència amb cola i esteneu-hi trossos de tovallons.
- Repetiu els passos 9-11 per a les inflorescències restants.
- Retalla 6 fulls de paper ondulat: enganxa'n 4 a les tiges i la resta a les vores.
- En alguns llocs de les voluminoses inflorescències, apliqueu taques de pintura d'aquarel·la rosa.
Tots els nens de 7 anys poden fer l'aplicació "Eruga". El procés de creació requereix poc temps, per la qual cosa és adequat per mantenir un nen ocupat durant un curt període de temps.
Com fer-ho:
- Retalla diversos cercles de la mateixa mida i de diferents colors.
- Enganxa els cercles un darrere l'altre sobre el cartró. Si voleu, disposeu els cercles amb elevacions, com si una eruga s'arrossegava.

- Al primer cercle, dibuixa un somriure, enganxa els ulls i acaba de dibuixar les pestanyes.
- Enganxa les banyes: dos triangles.
Per a nens de 2r a 4t de primària
Les figures estudiades per nens de fins a 11 anys els permeten crear dibuixos complexos i interessants. Fer combinacions de formes geomètriques i retallar petites peces desenvolupa la motricitat fina. En particular, l'aplicació "Mice" hi contribueix.
Peces necessàries per al vostre primer ratolí:
- El semicercle gris és el cos.
- 2 cercles negres de mides diferents: el nas i l'ull.
- 2 cercles grisos idèntics: orelles.
- 2 trossos de filferro negre: bigotis.
- Un tros de fil blanc gruixut és la cua.
Primer cal enganxar una orella a la base, després el cos, que se superposa lleugerament a l'orella, i després la resta de les parts.

Peces necessàries per al segon ratolí:
- L'oval gris amb extrems punxeguts és el cos.
- 2 cercles grisos: orelles.
- 2 petits cercles negres – ulls.
- El cercle negre més gran és el nas.
- 2 trossos de filferro negre: bigotis.
- Un tros de fil blanc gruixut és la cua.
Un tros de formatge és un triangle equilàter groc. Cal doblegar-lo per la meitat i enganxar-lo. Dibuixa cercles al doble triangle i retalla'ls amb unes tisores d'ungles. Retalla la part inferior del triangle de manera que el triangle quedi equilàter.
Com organitzar els elements en un full:
- Enganxa el formatge de manera que la cantonada apunti cap a la diagonal superior dreta.
- Enganxa el primer ratolí per sobre del formatge, més a prop de la base. Baixa la cua cap avall i cap a la dreta perquè quedi sobre el formatge.
- Col·loca el segon ratolí sota el formatge, més a prop del seu extrem, de manera que el seu nas gairebé toqui la vora del formatge.
El fons pot ser no només de cartró llis, sinó també de cartró amb un patró inusual (quadres de camisa o cercles). Els nens de 8 a 10 anys són capaços de combinar diferents elements per crear històries complexes.

Per crear l'aplicació "Espai", heu de fer els següents models de coets:
- Retalla el cos del coet que es mostra a la foto següent.
- Retalla 3 cercles de la mateixa mida en un color contrastant.
- Retalla 3 cercles més petits.
- Enganxa un cercle del punt 3 a cada cercle del punt 2. Això crearà finestres.
- Enganxa les finestres al cos del coet.
Segon model de coet:
- Retalla el cos del coet de la foto.
- Retalla dos cercles de mides diferents.
- Enganxa-ho en un cercle petit dins d'un de gran.
- Retalla un oval, talla'l en 4 parts (2 parts són les ales del coet).
- Enganxa la finestra i les ales al cos del coet.
Cal fer diversos coets i enganxar-los al full perquè volin en diferents direccions. Ompliu la zona restant amb petits cercles i estrelles. En els dibuixos animats, el foc o el fum surten de la cua dels coets, que es poden representar com a ovals o com a detall en espiral.
Aplicació geomètrica "Transport"
Les figures de formes geomètriques formen imatges completes quan es distribueixen correctament.
A continuació es mostren aplicacions per a diferents tipus de transport. L'aplic "Tren" consta de dos tipus de vagons: el primer vagó i la resta. Primer, s'enumeren les xifres necessàries per al primer vagó.
| Aplicació | Figures que s'utilitzen en el procés de creació d'una aplicació | La part del transport que representa la figura | Característiques de la ubicació |
| "Tren" | Rectangle | Marc | El semicercle és a l'esquerra del rectangle |
| Semicercle | |||
| Rectangles grans i petits | Cabina del conductor | Un dels rectangles és una finestra | |
| Triangle | Canonada | Part de la figura està coberta pel rectangle del cos | |
| Triangle més petit | Llanterna | Parcialment cobert pel semicercle del cos | |
| Rectangle | Distància entre eixos | Enganxat sota el cos | |
| 3 cercles | Rodes | Estan situats sota el cos i estan units a un rectangle. | |
| Cercle més gran | Roda | Està enganxat sota la cabina del conductor, cobrint-la parcialment. | |
| Rectanguls prims | Cadenes que connecten els cotxes | — | |
| Rectangles | Vagons | — | |
| 4 voltes 1 cotxe | |||
| "Autobús" | Rectangle gran | Marc | — |
| 2 cercles | Rodes | Cobreixen part del cos i es troben més a prop de les vores del rectangle. | |
| 2 rectangles | Portes | Estan situats a prop de les rodes. | |
| 4 rectangles més prims | Portes de finestres | Hi ha 2 finestres per a cada porta | |
| 2 quadrats | Finestres al cos | Les finestres quadrades es troben a les vores de les portes i una finestra rectangular entre elles. | |
| Rectangle | |||
| "Vaixell" | Triangle amb vores tallades | La part principal del vaixell | — |
| 3 cercles | Finestres | — | |
| Rectangle prim i llarg | Un pal al qual s'uneixen les veles | Enganxat a l'esquerra del mig del triangle principal | |
| Triangle | Navegar | Estan enganxats a banda i banda del pal. | |
| Semicercle | |||
| Quadrat | Bandera | Situat a la part superior del pal | |
| triangles rectangles | |||
| "Camió" | 2 rectangles de diferents mides | Cabina del conductor i part davantera | El rectangle més petit està unit al costat del més gran. |
| Quadrat | Finestra | — | |
| Rectangle | Cos | — | |
| 2 cercles | Rodes | Un cercle es troba sota la cabina del conductor i el segon, sota la carrosseria. Alguns dels cercles se superposen a la part del camió a la qual estan units. | |
| Triangle | Càrrega | — |
Aplicacions de figures geomètriques "Animals"
Fins i tot les més petites poden representar animals.


L'aplicació "Mico" consta de les següents figures:
- Cos ovalat.
- 4 ovals prims: braços i cames.
- L'oval prim i corbat és la cua.
- El cercle és la cara.
- 4 cercles (2 petits i 2 mitjans) – orelles.
- El cercle és el nas.
- 2 cercles blancs i 2 negres: ulls.

L'aplicació "Ós" consta de les mateixes figures, però s'utilitzen 2 semicercles com a orelles i la cua no és visible.

Aplicació "Pollastre":
- Retalla 2 ovals i enganxa'ls a una certa distància l'un de l'altre. Aquests ovals es convertiran en les ales.
- Retalla un oval groc: el cos del futur pollastre. Enganxa el cos entre les ales de manera que se superposi a una part de les ales.
- Enganxa un cercle a sobre: la cara del pollastre.
- Retalla un petit cercle taronja. Enganxa un cercle negre encara més petit a l'interior.
- Enganxa els cercles enganxats al costat de la cara, com si el pollet mirés cap a la dreta o l'esquerra.
- Retalla 3 triangles vermells.
- Enganxa un triangle al costat de la cara al costat de l'ull; aquest triangle serà el bec.
- Enganxa els triangles restants sota el cos: aquestes són les potes de l'ocell.
- Enganxa un triangle groc en angle recte al costat on no es troba el bec. Aquest triangle és la cua.
Per completar la imatge, cal afegir herba, formada per ovals de diferents mides i longituds, al costat de les potes del pollastre. Així, sembla que l'ocell estigui corrent pel camp.

L'aplicació d'elefant consta de les parts següents:
- El cercle és un cos.
- Els rectangles són les potes.
- Els semicercles són peus.
- El triangle prim és la cua.
- El semicercle més gran és l'orella.
- Un petit cercle és el cap.
- Rectangle - tronc.
- Cercles blancs i negres: ull.
Es recomana deixar que el nen esculli per si mateix quin animal vol representar i com ho vol fer.
Dibuixos de formes geomètriques: tasques per a nens
Després d'haver estudiat formes geomètriques, el nen ha d'entendre com combinar-les en dibuixos complexos.
Les figures a partir de formes geomètriques són la primera etapa d'estudi. La segona etapa consisteix a plegar figures en dibuixos dels objectes que els envolten.
Variants d'exercicis per avaluar els coneixements sobre formes geomètriques:
- Imprimeix un formulari que mostri diversos objectes. La tasca del nen és anomenar les figures que veu en els objectes presentats.
- Divideix el full en 2 parts. A l'esquerra, dibuixa parelles de dues figures idèntiques. L'exercici consisteix en què el nen dibuixi al costat dret figures que es poden obtenir a partir de parelles de figures a l'esquerra (2 triangles rectangles – un rectangle).
- Imprimiu formularis amb imatges de diversos objectes (tren, vaixell, arbre de Nadal amb boles). Tasca: compta el nombre de cada figura de les imatges.
- Imprimiu formularis amb imatges dibuixades i un nombre determinat d'alguna figura especificada. Cal trobar un dibuix que contingui el número especificat d'una figura determinada.
Les tasques enumerades anteriorment ajuden al nen a recordar les xifres i a aprendre a comptar correctament. Un nen comença a familiaritzar-se amb les formes geomètriques des que neix, aprenent cada cop més informació sobre el món que l'envolta. Es recomana que l'entrenament es realitzi en forma de joc, creant diferents combinacions de figures amb el nen.
Autor: mariamur1
Format de l'article:Natalie Podolskaya
Vídeo sobre formes geomètriques
Com fer figures a partir de formes geomètriques: manualitats per a nens en aquest vídeo:
