Escaneig d'icosaedre per enganxar: plantilles A4, A3 amb marges, dimensions. Esquemes

Les figures fetes de paper poden ser diferents.. No obstant això, la majoria de les vegades es dóna preferència a les formes geomètriques. Un d'aquests és l'icosaedre (un patró per enganxar), que es pot anomenar complex i simple alhora. Complex perquè té moltes cares (20 peces) i encara més arestes (30 peces). Simple perquè és completament simètric respecte al seu centre.

Descripció de la figura

L'icosaedre (el patró per enganxar es mostra a continuació a l'article) és una figura que va rebre el seu nom fa uns 100 anys. Prové del numeral grec antic "ikosi", que es tradueix com a "20". L'altra part del nom deriva de la paraula "hedra", que significa "vora". Resulta que el nom es pot traduir del grec com a "de 20 cares".

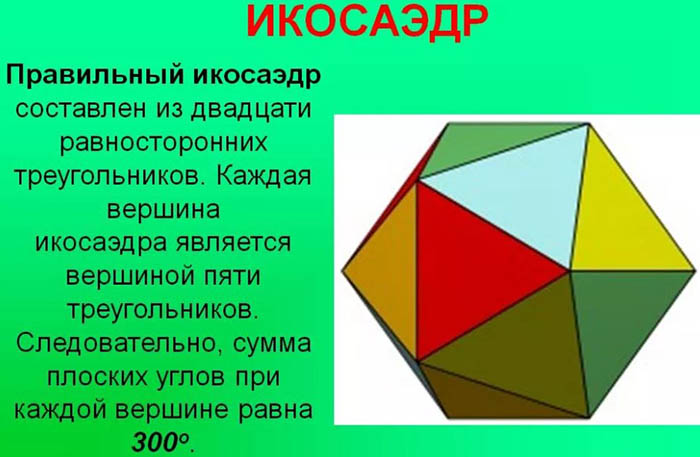
Perquè un cos geomètric tridimensional es pugui anomenar icosaedre regular, ha de complir les condicions següents:

• ha de tenir exactament 20 cares (ni més ni menys);
• cadascuna d'aquestes cares ha de ser un triangle regular. En geometria, un triangle s'anomena regular si tots els seus angles són iguals. Cada angle d'aquest triangle té un valor de 60 graus.

L'icosaedre és un poliedre regular i és un dels cinc sòlids anomenats "platònics".

Les seves altres característiques són les següents:

• el nombre de costats de cadascuna de les 20 cares és 3;
• nombre de vèrtexs (punts de connexió dels costats de les cares) – 12;
• el nombre d'arestes (costats de les cares) que convergeixen a cada vèrtex (punt) és 5;
• nombre total de costelles: 30;
• nombre d'eixos de simetria: 15;
• nombre de plans de simetria – 15.

Tanmateix, totes aquestes característiques es deriven de les dues principals esmentades anteriorment. Si una figura té 20 cares i si cada cara és un triangle regular, aleshores ja serà un icosaedre regular real amb totes les seves propietats.

L'icosaedre (el patró per enganxar no és difícil ni tan sols per a principiants) és una figura l'àrea de la qual és fàcil de determinar, malgrat el gran nombre de cares. A més, es pot representar com una àrea d'escombrat. Si es coneix l'àrea d'1 dels 20 triangles que són les cares de la figura, n'hi haurà prou amb multiplicar aquest nombre per 20.

Per exemple, si l'àrea de cada triangle és de 4 cm², l'àrea total de totes les superfícies de l'icosaedre serà igual a 80 m². Per fer això, cal multiplicar 4 per 20.

Tipus principals

L'icosaedre que es pot fer de paper pot ser diferent.

Per exemple, si:

• Si només feu servir un color de paper a la vostra obra, la figura resultarà ser d'un sol color;
• serà paper de colors, podeu fer un icosaedre multicolor, que jugarà amb diferents colors i quedarà més bonic.

Sovint es fa un icosaedre, que sembla una pilota de futbol en color, amb triangles blancs alternant amb triangles negres. En realitat no serà una pilota, ja que està lluny de ser rodona. Més difícil d'executar és l'icosaedre, que té forma d'estrella. Aquí ja hi ha facetes que destaquen sobre el fons d'altres.

El més bonic és l'icosaedre, decorat amb diversos elements decoratius. Poden ser qualsevol decoració: alguna cosa brillant, brillant, alguna cosa que es pugui enganxar fàcilment a la superfície del paper. Aquest icosaedre es pot utilitzar com a joguina de Cap d'Any i penjar-lo a l'arbre de Nadal.

Hi ha innombrables icosaedres en geometria. Alguns d'ells tenen més simetries, mentre que d'altres, en canvi, són menys simètrics. El més comú és l'icosaedre regular, és a dir, aquell que té exactament 20 cares idèntiques. En matemàtiques, un icosaedre regular es pot anomenar cos convex o no convex.

En qualsevol cas, cadascun d'ells té 20 cares i 1,5 vegades més arestes. Tots dos tenen el que s'anomena simetria ixosaèdrica. Tanmateix, sovint és la forma convexa la que s'anomena icosaedre regular, mentre que la forma no convexa entra dins la categoria de grans icosaedres.

L'icosaedre (escanejat per enganxar) es pot representar amb les opcions següents:

Figura	Descripció
icosaedre convex	Té 20 cares i 12 vèrtexs. Aquest sòlid geomètric té un poliedre dual. S'anomena dodecàedre regular. Té 3 cares regulars de 5 costats al voltant de cada vèrtex.
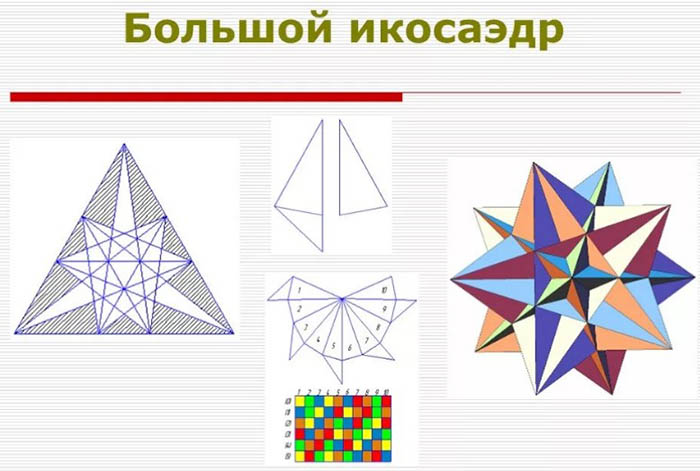
Gran icosaedre	Té exactament 20 cares, cadascuna de les quals és un triangle regular. Tanmateix, el seu vèrtex no és un 5-gon, sinó un pentagrama. És per aquest motiu que les arestes s'intersequen geomètricament. Quan s'intersequen, no es formen noves arestes. El poliedre dual del gran icosaedre és el gran dodecaedre. Té 3 cares concentrades al voltant de cada vèrtex, cadascuna de les quals és un 5-gon.
Icosaedres estrellats	Si les cares o arestes d'un políedre s'expandeixen, quan es toquen, es forma una estrella. Això passa simètricament, de manera que el cos resultant té les mateixes simetries que les figures originals. L'obra científica de Coxeter "59 icosahedra" enumera gairebé 60 varietats estrellades d'aquests políedres. Molts d'ells tenen una faceta separada en cadascun dels 20 plans. Molts altres cossos tenen més d'una cara al pla. Es poden formar fusionant políedres més simples.
Pseudoicosaedre	Un icosaedre regular que està retorçat, cosa que fa que es redueixi la seva simetria.
Icosaedre de Jessen	Si un cos geomètric tridimensional té 12 cares, cadascuna de les quals és un triangle isòsceles, i aquestes cares estan disposades de manera que formen un cos no convex, aleshores aquesta figura ja s'anomenarà icosaedre de Jessen (o icosaedre ortogonal). Té angles rectes amb dos costats. Una de les seves característiques és que és equidescomponible amb un hexàgon, cada cara del qual és un quadrat. Això significa que es pot dividir en petits políedres i després utilitzar-lo per formar un hexàgon amb cares de la mateixa mida. Un hexàgon d'aquest tipus és un cub.

Com fer un icosaedre regular de paper?

El desenvolupament per enganxar l'icosaedre per a la fabricació requerirà la preparació dels següents materials i eines:

• paper. Pot ser ondulat, blanc o de color. La seva densitat també pot variar;
• tisores. Necessari per retallar figures de les mides i formes requerides;
• cola. La millor opció és el PVA normal, ja que triga molt a assecar-se, cosa que és suficient per eliminar possibles errors;
• governant. Sense això, serà molt difícil doblegar el paper uniformement al llarg de la línia de plec.

També podeu utilitzar materials addicionals per decorar les vostres manualitats de paper. És qüestió de gust i imaginació.

Després de preparar tots els materials i eines, podeu procedir directament al procés creatiu.

El treball es desenvolupa en les següents etapes:

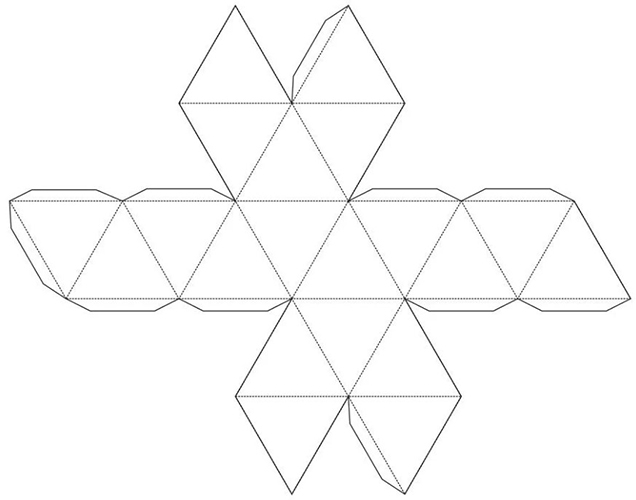
1. Imprimeix la plantilla acabada en una impressora i transferir-ho al material preparat. Cal anar amb compte a l'hora de fer el trasllat. En cas contrari, les marques seran incorrectes, cosa que significa que la figura en conjunt quedarà desigual o no serà res en absolut. És molt recomanable utilitzar un regle.
2. Comença a retallar la plantilla. Les tisores han de passar estrictament per les línies de punts. Altrament, no serà possible enganxar tots els elements de la figura. Tanmateix, no us heu de precipitar, perquè la plantilla es pot danyar fàcilment per un moviment descuidat. És important que tots els elements triangulars de la plantilla tinguin costats iguals. Aquesta és una de les principals propietats de l'icosaedre. És tan important i obligatori com la condició que tots els costats d'un mateix quadrat siguin sempre iguals. Si es viola aquesta regla, la diferència entre els bàndols serà molt notable.
3. Després de retallar el blanc, comenceu a doblegar la figura. Aquí definitivament es necessita un governant. Els punts de plec es mostraran com a línies contínues i l'enganxament s'ha de fer al llarg de les línies de punts. L'objectiu principal és connectar correctament totes les cares dels elements triangulars de la figura. Si per alguna raó no teniu cola PVA a mà i, en canvi, trobeu un adhesiu d'assecat ràpid, heu de recordar que no hi ha marge d'error. Si connecteu les peces incorrectament i la cola s'asseca en qüestió de segons, ja no serà possible separar els elements. Si treballeu amb cola PVA, haureu de prémer fort a cada junta. Després d'aplicar la cola, manteniu les peces pressionades entre si durant uns 20 segons.
4. Decorar el producte acabat. Per a això podeu utilitzar pintures, retoladors, llapis i pastels. També pots enganxar un fil a la figura acabada per poder penjar-la. Sovint aquestes manualitats de paper s'utilitzen com a decoració d'arbre de Nadal per a l'Any Nou.

L'ús de l'icosaedre pot ser diferent. Pot complir no només una funció estètica, sinó també una funció pràctica.

icosaedre multicolor

L'icosaedre (el patró per enganxar es pot acolorir) multicolor pot convertir-se en una bona ajuda visual a l'hora d'estudiar els tons de color amb els nens més petits.

Per treballar en la creació d'un icosaedre multicolor, necessitareu els següents materials i eines:

• plantilla ja feta (es pot trobar fàcilment a Internet);
• paper de colors (si no en teniu, podeu pintar paper blanc amb retoladors, pintures o llapis, cosa que serà interessant i entretinguda per als nens);
• cola (es recomana utilitzar PVA d'assecat prolongat);
• tisores.

Un cop tot estigui preparat, podeu procedir directament al procés de creació, que consta de les següents etapes:

1. Feu un espai en blanc amb una plantilla. Pel que fa al nombre de colors diferents, pot ser qualsevol a discreció de la persona que fa l'artesania. Tanmateix, com més diferents colors brillants hi hagi, més li agradarà aquest producte al nen. Podeu prendre, per exemple, els colors primaris de l'arc de Sant Martí. Podeu afegir uns quants colors més o, al contrari, eliminar els que semblen innecessaris (per exemple, no cal que una figura tingui blau i blau clar).
2. Connecteu tots els elements amb cola PVA de llarga durada.

Icosaedre estrellat

L'icosaedre estrellat és un dels més difícils de fer. Tanmateix, tota la dificultat rau en el fet que cal tenir molta paciència. La feina trigarà molt de temps.

A més de paciència, necessiteu:

• tisores;
• paper de colors;
• cola.

Podeu preparar alguns elements decoratius per decorar el producte acabat. Poden ser qualsevol objecte que sembli bonic: fils de colors, cintes, perles adhesives.

Un cop preparat tot el necessari, podeu procedir directament al procés creatiu, que consta de les etapes següents:

1. Retalla 30 quadrats de paper amb costats de 5 cm cadascun. Cada quadrat d'aquest tipus ha de tenir una superfície de 25 metres quadrats. vegeu. En aquest cas, hauríeu de fer servir paper de 3 colors. Poden ser qualsevol tons, per exemple, verd, blau i vermell. Al final hi hauria d'haver 10 quadrats de cada color.
2. Quan s'hagi retallat el nombre necessari de quadrats, podeu agafar-ne un i plegar-lo per la meitat. Aleshores, cal doblegar cada meitat cap al mig, redreçar-la i plegar les cantonades oposades dues vegades.
3. Feu que el full de paper sembli la paparra clàssica, que sovint està feta de paper. Per fer això, doblegueu la cantonada gran des del costat inferior.
4. Agafa l'altre costat del quadrat. S'ha de girar i després plegar la part superior per formar un sobre. En aquest cas, el seu angle agut s'ha d'inserir dins del producte.

5. Continua treballant amb el primer quadrat. Ara que s'ha convertit en un sobre, cal plegar-lo per la meitat i plegar les orelles que sobresurten, dirigint-les cap a les cantonades exteriors dels triangles. A continuació, després de redreçar, es forma una unitat de muntatge.
6. Per fer la part més llarga de la feina, cal repetir els 5 passos descrits anteriorment amb cadascun dels 29 quadrats restants. Això requerirà molta paciència. Potser no és possible fer els 30 models necessaris alhora. Es recomana fer pauses en aquest procés creatiu.
7. Quan les 30 peces estiguin a punt, podeu agafar-ne una i ficar-ne la punta a la butxaca d'una altra (necessàriament d'un color diferent). En conseqüència, la cantonada d'aquest element hauria d'encaixar a la butxaca de la tercera part, que difereix en color de les altres dues. La cantonada de la tercera peça ha d'encaixar a la butxaca de la quarta peça, que serà del mateix color que la primera peça. D'aquesta manera, els colors s'alternaran.
8. Inseriu la punta de la tercera peça a la segona peça. La primera part s'hi inserix i la punta de la segona part es treu a la butxaca del primer enllaç.
9. Inseriu el segon trencaclosques dins del tercer, després el primer, i tot es tanca amb el tercer.
10. Munta tots els elements segons el diagrama anterior. Un cop l'últim element està al seu lloc, es pot considerar completa la llarga i minuciosa feina de fer l'icosaedre estrellat.

Icosaedre decoratiu

Aquest cos geomètric de 20 cares fet de paper amb la tècnica kusudama quedarà molt bé en un arbre festiu la nit de Cap d'Any. Per fer un icosaedre decoratiu, cal retallar 30 quadrats de paper. És millor si és de color groc clar.

Després d'haver preparat el nombre necessari de quadrats de paper, podeu començar el procés creatiu:

1. Agafeu un dels quadrats (són tots iguals, així que podeu agafar qualsevol), doblegueu-lo per la meitat i doblegueu els costats cap al mig.
   A continuació, la peça es desplega i es plega al llarg de la línia central. Cal plegar les vores cap al centre i després obrir-les de nou.
2. Doblegueu la peça de manera que el quadrat es converteixi en un triangle. Després d'això, s'ha de redreçar i les parts laterals s'han de doblegar cap a la línia central. Aleshores, una de les vores inferiors s'ha de plegar cap al costat. El resultat hauria de ser un córner. La vora oposada s'ha de plegar cap al centre per formar un nas punxegut.
3. Repetiu tot el procediment anterior, però ara amb el segon costat de la peça. El resultat és un quadrat amb un parell de brocs de forma triangular.
4. El trencaclosques s'ha de plegar longitudinalment, amb un dels dos triangles plegat cap endavant i l'altre en la direcció oposada.
   A continuació, cal redreçar la peça. Per fer això, cal estirar-ne els extrems. Això crearà el primer enllaç de l'icosaedre decoratiu. Tanmateix, hi hauria d'haver 30 enllaços d'aquest tipus en total, de manera que el procediment es realitza 29 vegades més.
5. Quan els 30 elements estiguin a punt, podeu començar a connectar-los. Això es fa de la següent manera: la punta d'una baula s'ha d'inserir a la butxaca de l'altra; després s'insereix la punta del tercer enllaç a la mateixa butxaca; i la punta del 4t està enfilada a través del 5è; aleshores el 1r s'insereix al 5è, donant lloc a un anell tancat.
6. Totes les puntes del següent pètal s'han de col·locar als espais entre els enllaços per formar un triangle.
7. Cada part ha de ser sotmesa a un procediment similar. Després de tancar el triangle final, es forma una figura preciosa que quedarà molt bé a l'arbre de Nadal.

Després d'haver entès com fer un patró de paper per enganxar un icosaedre, podeu començar a modelar-lo vosaltres mateixos, utilitzant una varietat de solucions de color, materials i decoracions.

Vídeo sobre com fer un icosaedre amb paper

Classe magistral sobre com fer un icosaedre amb forats: